Atenção
Fechar
As substâncias, em qualquer estado físico, possuem propriedades magnéticas e podem ser classificadas numa das seguintes categorias:
1) materiais diamagnéticos
2) materiais paramagnéticos
3) materiais ferromagnéticos
Quando se colocam diversas substâncias num campo magnético, pode-se observar que algumas se orientarão na direção do campo, ficando fortemente magnetizadas. Estas recebem o nome de ferromagnéticas. Outras se magnetizam fracamente, mas também se orientam paralelamente ao campo e são chamadas paramagnéticas e, finalmente, outras dispor-se-ão normais ao campo, caso este não seja uniforme e são as diamagnéticas. Como os efeitos magnéticos nas substâncias dia e paramagnéticas são relativamente fracos, elas são consideradas como materiais não magnéticos.
O diamagnetismo é uma propriedade inerente a todos os materiais e só não é detectável na presença de efeitos paramagnéticos ou ferromagnéticos mais intensos.
Langevin demonstrou que a aplicação de um campo magnético num sistema de elétrons em movimento de translação induz um momento magnético que se opõe ao campo externo. A variação do momento induzido com o campo é a suscetibilidade diamagnética. Tanto a teoria de Langevin como as observações experimentais demonstram que essa suscetibilidade é independente da temperatura.
Nos elementos que possuem órbitas eletrônicas incompletas, os momentos magnéticos resultantes dos movimentos de translação e de rotação dos elétrons podem não se compensarem e cada átomo no reticulado comportar-se-á como um dipolo magnético, com orientação a esmo. A aplicação de um campo magnético externo tenderá a orientar esses dipolos na direção do campo, o que constitui o efeito paramagnético. Nestas circunstâncias, explica-se a influência da temperatura neste efeito. No tratamento teórico do problema, Langevin calculou a relação entre o momento magnético induzido e a temperatura, obtendo resultado que se verifica com boa aproximação pelas determinações experimentais.
Em alguns casos, como por exemplo no do cobre, o paramagnetismo fraco dos elétrons das órbitas incompletas não contrabalança a contribuição diamagnética das órbitas internas, de modo que o efeito resultante é diamagnético. As figuras 181 e 182 esquematizam a distribuição das linhas de força dos materiais dia e paramagnéticos.
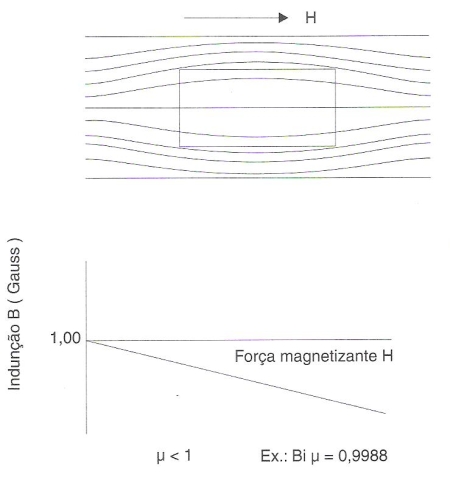
Fig. 181 – Distribuição das linhas de força na transição do ar ou do vácuo, para um material diamagnético. Diagrama B vs H para o mesmo material.
Os materiais ferromagnéticos diferem dos paramagnéticos por possuírem uma permeabilidade que pode atingir valores milhares de vezes maiores que a dos materiais paramagnéticos, cuja permeabilidade é constante e pouco superior a 1. Além disso, a permeabilidade dos materiais ferromagnéticos depende da intensidade do campo magnetizante, como mostra a figura 183.
Para a explicação do ferromagnetismo deve-se levar em conta dois fenômenos importantes:
1) que esse comportamento só se observa em 4 dos 92 elementos conhecidos, isto é, no ferro, cobalto, níquel e gadolínio;
2) que o elevado número magnético apresentado por esses elementos depende do campo magnetizante.
O estudo teórico do assunto levou à conclusão que o efeito ferromagnético depende do spin dos elétrons, de modo que cada elétron girando em torno de si próprio comporta-se, como no caso das substâncias paramagnéticas, como um dipolo elementar. Estes podem ser orientados paralelos aos campos externos, mas normalmente não estão completamente orientados. O estado de mínima energia num sistema atômico dá-se quando um certo número desses ímãs elementares está orientado numa direção e um número equivalente, em sentido oposto. A propriedade ferromagnética se manifesta quando o número de spins eletrônicos (momento magnético devido ao spin) paralelos ao campo aplicado ultrapassa o número de antiparalelos.
O fato do ferromagnetismo só ser observado nos 4 elementos citados não é acidental. Esses elementos de transição são caracterizados por possuírem órbitas de alta densidade eletrônica não saturadas (órbitas d e f), de modo que tal equilíbrio não se verifica. A teoria moderna, baseada na mecânica quântica, estabelece que, em determinadas condições, o estado de mínima energia nessas órbitas ocorre quando há uma preponderância de spins sobre antiparalelos. Essas condições são:
1) que o material esteja no estado sólido;
2) que a relação entre as distâncias interatômicas e os raios das órbitas citadas dentro de certos limites.
Aplicando essas condições a diversos elementos, Beth e outros pesquisadores verificaram que elas são satisfeitas pelos quatro elementos ferromagnéticos.
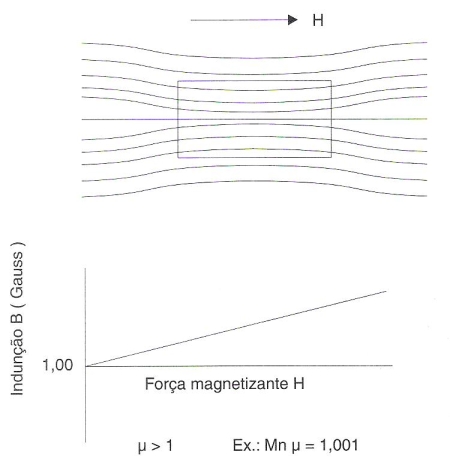
Fig.182 – Distribuição das linhas de força na transição do ar ou do vácuo para um material paramagnético. Diagrama B vs H para o mesmo material.
3.1 – Domínios ferromagnéticos
As condições descritas no parágrafo anterior, quando satisfeitas, permitem a interação entre elétrons das órbitas 3d de átomos vizinhos tendendo a orientá-las magneticamente numa direção. Esse efeito se estende a pequenos volumes do cristal, delimitando no seu interior regiões da ordem de 10-9 cm2, chamados “domínios”. Nessas condições, cada cristal ou grão de um metal ferromagnético, mesmo na ausência de um campo magnetizante externo, acha-se dividido em domínios ferromagnéticos, com as características de dipolos elementares. O estado macroscópico de desmagnetização é explicado como um resultado estatístico da orientação a esmo dos domínios ferromagnéticos.
Uma demonstração prática dessa teoria foi dada por Bitter, que obteve desenhos em superfícies polidas de cristais ferromagnéticos pela distribuição zonada de Fe2O3 em pó. Mais tarde, determinando-se as curvas de magnetização por métodos eletrônicos sensíveis, observou-se que elas apresentam descontinuidades durante a magnetização, que correspondem às que resultariam de mudanças de direção em domínios da ordem de grandeza dos propostos pela teoria.
3.2 – Curva de magnetização
Uma curva de magnetização, como a que se vê na figura 184, dá a variação da indução B com a força magnetizante H.
Nessa figura, o trecho que parte da origem e atinge o ponto mais elevado da curva, corresponde à “curva de magnetização” e o ciclo fechado pela linha externa representa o “ciclo de histerese” que decorre do fato dos fenômenos de magnetização não serem fenômenos reversíveis, pois com a diminuição do campo H, B não diminui de acordo com a curva de magnetização.
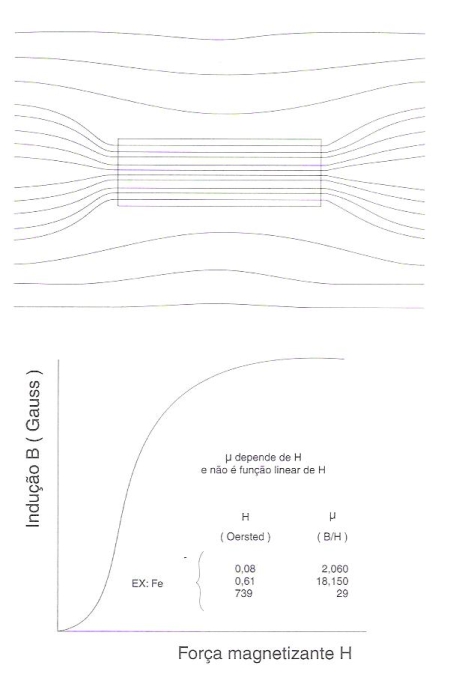
Fig. 183 – Distribuição das linhas de força na transição do ar ou do vácuo, para um material ferromagnético. Diagrama B vs H para o mesmo material.
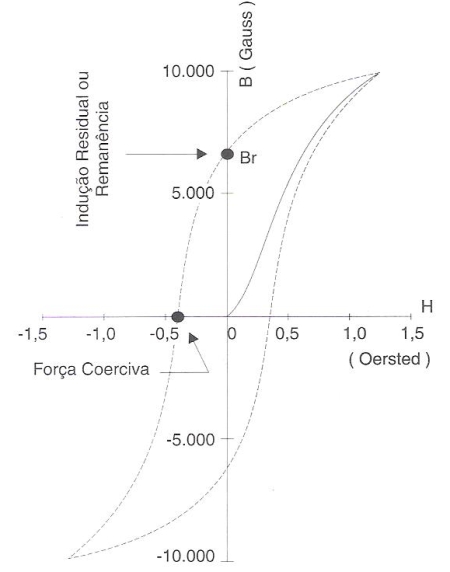
Fig. 184 – Curva de magnetização e ciclo de histerese do ferro.
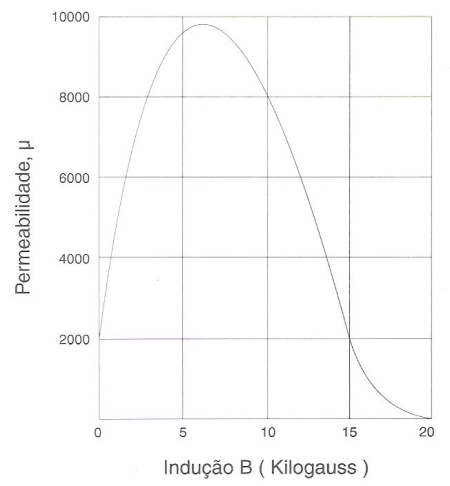
Fig. 185 – Relação entre a permeabilidade e a indução magnética do ferro puro.
O coeficiente angular das retas traçadas da origem a pontos da curva de magnetização representa a permeabilidade do material, na correspondente intensidade do campo magnetizante, ou da indução B. Pelo desenvolvimento da curva de magnetização do ferro puro, pode-se ver que a permeabilidade varia com o campo magnetizante de um modo não linear, passando por um máximo, que corresponde à tangente tirada da origem do cotovelo da curva. A figura 185 mostra, ainda no caso do ferro puro, a variação da permeabilidade µ com a indução B.
Como B está relacionado a H pela expressão B = H + 4¶ I
B cresce ilimitadamente com H.
Voltando à curva da figura 184 com a eliminação do campo H, o valor B não volta a zero, mas reduz-se a um valor que recebe o nome de “indução residual”, ou “remanência”. Essa remanência representa a magnetização retida pelo material. Se, em seguida, for aplicado um campo de sentido oposto, o valor da magnetização residual decrescerá progressivamente até zero. O valor do campo desmagnetizante que anula a magnetização residual recebe o nome de “força coerciva”. Para campos desmagnetizantes mais intensos, o ciclo se repete de modo análogo e simétrico ao descrito.
A irreversibilidade dos fenômenos de magnetização exige um consumo de energia para que um dado volume de material percorra um ciclo de histerese. No caso de campos continuamente alternantes, como os que ocorrem nos transformadores, a cada ciclo da tensão corresponderá uma perda proporcional à área do ciclo de histerese do material do núcleo. Por outro lado, as variações do fluxo magnético geram no núcleo correntes elétricas que também se dissipam na forma de calor e que recebem o nome de “correntes de Foucault”.
A soma da perda devida à histerese com a perda devida às correntes de Foucault recebe o nome de “perda do núcleo” e constitui uma característica importante para a classificação dos materiais para núcleos transformadores.
3.3 – Características das curvas de magnetização
Na parte inicial das curvas de magnetização os fenômenos são praticamente reversíveis e B varia de um modo aproximadamente linear com H. Nessa região, os domínios com orientação favorável, em relação ao campo magnetizante, crescem às expensas dos domínios vizinhos desfavoravelmente orientados, pelo movimento de seus contornos, mantendo sua orientação com relação aos eixos cristalográficos.
A parte média da curva é a região onde as perdas por histerese ocorrem. Aqui a magnetização é irreversível e resulta de mudanças bruscas na orientação dos domínios, associadas ainda a movimentos dos contornos. O cotovelo da curva corresponde à orientação de todos os domínios paralelamente aos eixos cristalográficos que mais se aproximam da direção do campo. Na parte superior da curva, onde a magnetização tende à saturação, o fenômeno é novamente reversível. Ele resulta da progressiva orientação dos domínios no sentido do campo.
3.4 – Ansiotropia dos materiais magnéticos
De um modo geral, observa-se que nos materiais policristalinos a suscetibilidade magnética é idêntica em todas as direções. Ao se considerar, porém, um cristal isolado, ver-se-á que ele apresenta maior ou menor tendência para magnetizar-se de acordo com determinadas direções cristalográficas. As figuras 186 e 187 ilustram essa afirmação. No caso do ferro (fig. 186), as direções [100] são as de maior suscetibilidade, ao passo que para o níquel (fig. 187) as direções [111] são as mais favoráveis.
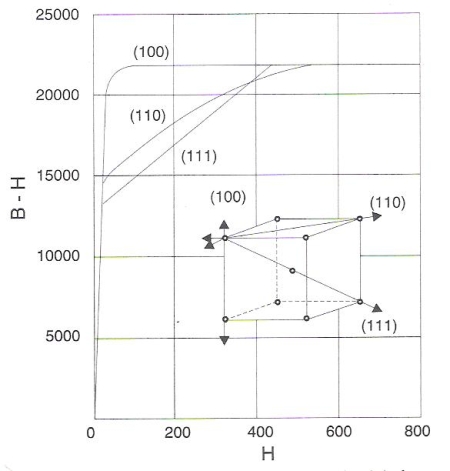
Fig. 186 – Anisotropia magnética de um cristal de ferro.
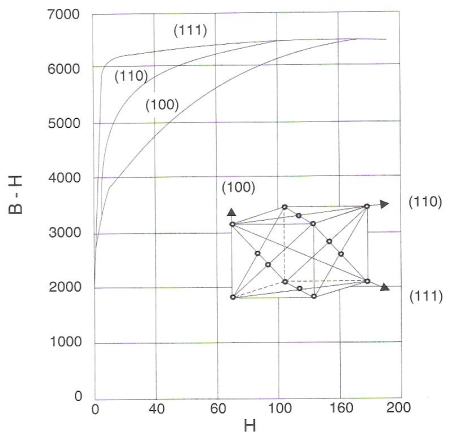
Figura 187 – Anisotropia magnética de um cristal de níquel.
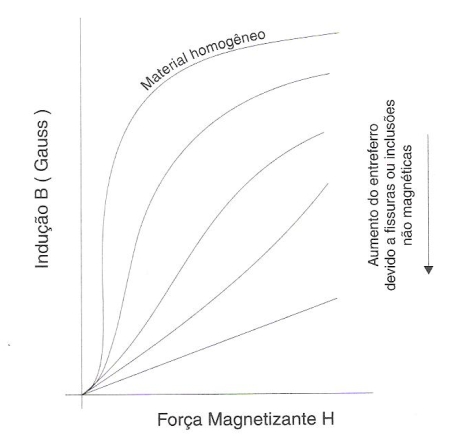
Fig. 188 – Influência da concentração de fissuras ou inclusões, na curva B vs H de um material ferromagnético.
Essa particularidade não teria importância prática se certos materiais magnéticos, como as ligas Fe-Si, não manifestassem orientações preferenciais. Certos metais e ligas metálicas quando encruados por laminação até determinadas percentagens de redução, ao se recristalizarem por recozimento, desenvolvem os novos grãos com seus eixos cristalográficos em orientações preferenciais. Nessas condições, o comportamento ansiotrópico dos cristais e a orientação preferencial desses cristais podem propocionar a um produto melhores propriedades magnéticas em determinadas direções. É o caso das chapas Hipersil (Fe com 3,25% de Si) para transformadores.
3.5 – Efeito de inclusões, fissuras e constituintes não magnéticos
A força magnetizante efetiva Hef é constituída por duas parcelas: Hf, que representa a intensidade do campo externo e Hd, que representa os campos desmagnetizantes.
Os campos desmagnetizantes são os campos que se formam nos entreferros naturais, ou resultantes de trincas internas e nas inclusões e constituintes não magnéticos. O aumento desses defeitos, ou desses constituintes, diminui a força magnetizante efetiva e isso altera a curva de magnetização, como mostra a figura 188.
3.6 – Influência da temperatura nas propriedades ferromagnéticas
Ponto Curie – Opondo-se às forças ordenadoras das interações atômicas, que promovem a formação dos domínios ferromagnéticos, existem forças provocadas pela agitação térmica, que podem causar o desaparecimento desses domínios. Como estas aumentam com a temperatura, há, para todos os materiais ferromagnéticos, níveis de temperatura acima dos quais o efeito dispersivo da agitação térmica anula a tendência orientadora das forças de interação atômica, de modo que o material perde suas propriedades ferromagnéticas. Essa temperatura de transição recebe o nome de “ponto Curie”.
Resfriando-se o material abaixo do “ponto Curie”, suas características ferromagnéticas são recuperadas. A figura 189 mostra a variação da intensidade de saturação do ferro com a temperatura.
3.7 – Magnetoestricção
A magnetoestricção abrange todas as mudanças de dimensões que sofrem os materiais ferromagnéticos quando submetidos a campos magnetizantes. Esse fenômeno recebe várias denominações, como por exemplo, “efeito Joule”, quando se trata da variação do comprimento da peça em campos transversais; “efeito Barret”, quando for a variação do volume e “efeito Wiedemann” quando as variações de dimensão devido a campos radiais provocam movimentos de torção.
A figura 190 mostra a variação do efeito Joule nas ligas Fe-Ni para diferentes forças magnetizantes.
Os materiais que se alongam quando submetidos a um campo magnético possuem magnetoestricção positiva. Nestes materiais a permeabilidade aumenta devido a deformações elásticas.
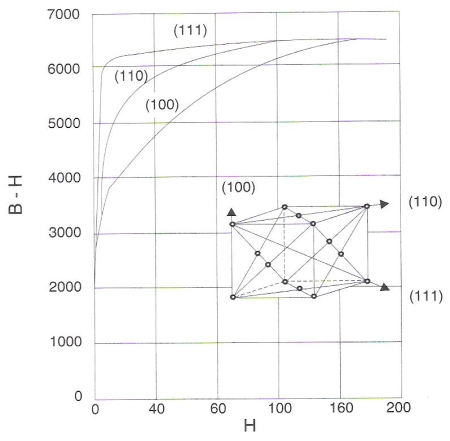
Fig. 189 – Perda das propriedades ferromagnéticas do ferro, no aquecimento.
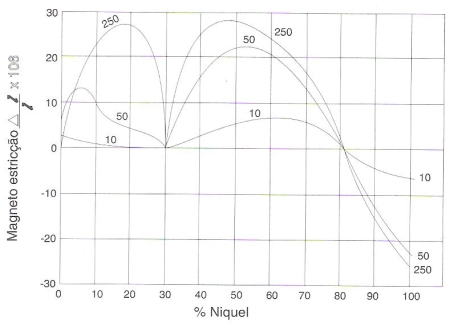
Fig. 190 – Magnetoestricção do sistema Fe-Ni.
Tais materiais têm tido aplicação em eletrônica, na fabricação de osciladores e filtros. No campo da tecnologia, sua aplicação mais interessante é para transformar energia elétrica de freqüência ultrassônica em pulsações mecânicas com a mesma freqüência como, por exemplo, nas máquinas perfuradoras para materiais extremamente duros, onde tais dispositivos são utilizados para impulsionar partículas de abrasivo contra o material a ser perfurado.